2025. 3. 21. 09:58ㆍPaper Review/Large Language Model (LLM)
Ishaan Gulrajani and Tatsunori B. Hashimoto. 2023. Likelihood-based diffusion language models. In Proceedings of the 37th International Conference on Neural Information Processing Systems (NIPS '23). Curran Associates Inc., Red Hook, NY, USA, Article 730, 16693–16715.
전통적인 LLM, 즉 auto-regressive 모델링 기법과 diffusion 모델링 기법을 비교하고 싶은데, diffusion 모델링 방법 자체가 언어 모델에서 개발된 학습 기법이 아니다보니 사람마다 해석하는 시점? 관점?이 다른 것 같아요.
그러다보니 어떤 diffusion 모델링이 더 적절할 것인가?로 묘하게 주제가 틀어지는 느낌도 받아 논문을 읽는데 속도가 나지 않는 것 같네요.
(논문 초반을 읽다 임시저장한 글만 몇번째인지.. 사공이 많아 배가 산으로 가고 있습니다.⛰️)
이번 논문은 NeurIPS 2023년도에 등재된 논문입니다.
Plaid라는 새로운 언어 모델을 소개하고 있어요.
2022년도 Diffusion-LM Improves Controllable Text Generation 논문에 참여했던
저자가 작성한 논문이라 모델 자체는 많은 특성을 공유하고 있는 듯 했습니다.
(이번에는 배가 산으로 가더라도 끝까지 밀려올려 보겠어요!!)
이번에는 산으로 가는 김에 새로운 색을 써봤습니다.
초록색은 제가 구체적으로 생각해본 예시입니다.
예시를 보지 않더라도 이해가 쏙쏙 되신 분들은 넘어가주세요.
Terminology
확산 언어 모델에 대한 설명을 쭈욱 읽다보니 쭈욱 읽을 수 없게 만드는 용어들이 많이 등장합니다.
이런 용어들에 대한 개념을 조금 정리하면 논문들에 대한 이해가 조금은 쉬워지지 않을까 합니다. (쉬워지진 않아요.. 그래도 읽을 수 있다?)
일단 이 논문에서 핵심은 "가능도 (Likelihood)" 이기 때문에 이 단어에 집중을 해보았습니다.
그냥 인터넷에서 쳐서 나오는 수준으로는 제가 이해하지 못하더라고요.
가능도란 모델이 특정 데이터를 생성할 확률을 의미합니다. 즉, 정답 토큰에 대해서 그 토큰을 생성할 확률이 높으면 좋은 모델이고, 반대로 낮다면 성능이 낮은 모델이 되겠죠. 그렇기 때문에 가능도를 기준으로 모델의 성능을 비교할 수 있는 거예요.
예를 들어 다음과 같은 문장을 생성한다고 가정합니다.
"과일 가게에서 토마토와 당근을 샀다."
과일 가게에서: 0.4 (40%)
토마토와: 0.3 (30%)
당근을: 0.7 (70%)
샀다.: 0.5 (50%)
전체 가능도 (Likelihood) = 0.4 * 0.3 * 0.7 * 0.5 = 0.042 (4.2%)
전체 가능도가 4.2%이기 때문에 자연스럽게 문장을 생성할 수 있는 확률이 낮고, 그 만큼 아직 문장을 만드는 능력이 부족하다고 표현할 수 있습니다.
여기서 이런 가능도를 높이기 위한 학습 방법 중 하나가 바로 Maximum Likelihood Pretraining (MLE)입니다. 모델이 주어진 데이터를 가장 잘 설명할 수 있도록 확률값을 최대화하는 학습 기법입니다. 모델이 가능도를 최대화화도록 모델의 파라미터를 조정하는 방법입니다.
1 Introduction
(논문이 전반적으로 수식에 대한 설명이 많아 그저 제가 삼킨대로 다시 작성하였습니다. 소화는 안되네요 🤢)
지금까지 대부분의 대규모 언어 모델들 (LLM)은 자기회귀 모델 (auto-regressive) 접근 방식을 따랐습니다. 문장을 왼쪽에서 오른쪽으로 차례대로 생성하며, 각 위치에서 다음 단어가 될 확률을 최대화하는 방식으로 학습하는 것이죠. 이를 최대 가능도 사전 학습 (Maximum-Likelihood Pretraining)이라고 부르며, 실제로 이러한 방식은 다양한 down-stream tasks에서 우수한 성능을 보였습니다. 하지만, 자기회귀 모델 특성상, 토큰을 한 번에 여러개씩 동시에 생성하기 어렵고, 토큰을 순차적으로 이어 붙여야 하다보니 Long range planning이나 Controllable generation을 수행하는데는 한계가 존재했습니다. (글에서 특정 부분만 수정하거나, 여러 단어를 동시에 고려해 전반적인 맥락을 조정하고 싶어도 쉽지 않은거죠.) 이러한 한계를 극복하기 위해 본 논문에서는 연속 확산 모델 (continuous diffusion model)이라는 새로운 방식을 언어 모델링에 적용합니다. 이전 논문들에서도 확산 모델에 대한 접근은 이뤄졌지만 가능도 관점에서 기존 모델들과 직접적인 비교가 이루어진 점이 해당 논문의 가장 큰 차별점이라고 할 수 있습니다.
3 The Plaid framework
3.1 Learned embeddings
자기회귀 모델에서 임베딩 연산은 신경망의 첫 번째 계층일 뿐입니다. 그러나 확산 언어 모델에서 임베딩은 보다 근본적인 역할을 합니다. 확산 언어 모델에서 임베딩은 서로 다른 토큰들이 생성되는 순서를 결정합니다. 임베딩 간 거리가 먼 토큰들은 역(추론)과정의 초기 단계에서 쉽게 구별되지만, 가까운 임베딩들은 낮은 노이즈 수준에서만 구별이 가능하기 때문입니다. (즉, 자기회귀 모델의 경우 임베딩이 어떤 연산에 활용되기 보다 단어 토큰이 입력되면 이를 모델이 이해할 수 있는 숫자형 벡터로 변환하는 역할을 수행합니다. 반면, 확산 모델에서는 노이즈가 낀 벡터를 복원할 때 복원 순서에 임베딩 간 거리가 영향을 미친다는 의미입니다. 우리가 어떤 문제를 대할 때 비교적 쉬운 문제부터 빠르게 푸는 것을 생각하면 이해가 되지 않을까합니다.) 임베딩 모델의 중요성에도 불구하고 이전 확산 모델에서는 이를 최적화하지 못하는 문제들이 있었습니다. 이에 반해, Plaid 손실 함수는 이산 데이터의 로그 가능도를 직접 최적화할 수 있도록 설계되었습니다.
3.2 Categorical reparameterization
엄청 어렵게 표현하고 있지만, 한 마디로 요약하면 재매개변수화를 통해 모델이 기억해야 할 메모리를 최소화한다는 의미입니다. (약간 과일가게 심부름을 갈때, 한 10가지 종류의 채소나 과일을 얘기하고 외우라고 하면 앞 글자를 따서 외워놓는 방식과 비슷한 거예요.) 모델 최적화를 위해 임베딩 벡터를 모두 암기하는 대신 토큰에 대한 소프트맥스 가중 평균으로 재매개변수화하여 동적으로 계산하는 것입니다.
임베딩 벡터는 뭐고, 또 토큰에 대한 소프트맥스 가중 평균은 뭘까? 이런 생각이 들겁니다.
만약 모델이 임베딩 벡터를 직접 기억해야 한다고 하면,
가정: 단어 수: 100,000개, 벡터 차원: 300? → 메모리 사용량: 100,000*300 = 30,000,000
모델이 하나의 단어마다 300차원 벡터를 암기하는 것을 의미합니다. (단어 수가 몇개든 어마어마한 양의 메모리가 될 거예요.)
로짓을 기억하고 계산을 통해 벡터를 생성 (재매개변수화)
모델은 고정된 임베딩 벡터가 아닌 각 단어의 확률을 계산하기 위해 로짓을 학습합니다.
이때, 로짓 벡터의 크기는 단어 수와 동일 합니다. (각 단어가 선택될 확률이니깐 당연하겠죠?)
모델이 기억하는건 실제 로짓 값이 아닌 로짓을 생성하는 함수 파라미터 입니다.
로짓 계산을 위한 함수 파라미터만 기억하면 실제 연산을 수행해서 임베딩 벡터를 추론할 수 있게되는 거죠.
3.3 Output prior
수식을 이해하는건 항상 너무 어려운 것 같아요.
사후 확률? 이렇게 부르는게 좀 어색해서 그냥 output prior로 하겠습니다.
위에서는 모델이 고정된 값을 기억하는 대신 이를 계산할 수 있는 함수를 기억해서 메모리를 절약하는 방법에 대해 다뤘습니다.
해당 함수는 일부분 output prior를 계산하는데도 사용이 됩니다.
논문에서는 어떤 식이 output prior를 계산하는 최적의 식이고, 식에 포함된 각 항이 뭘 의미하는지 간략하게 말하고 있습니다.
제가 알아들을리 없습니다.
output prior를 사용하는 이유는 뭘까요?
output prior는 모델이 특정 토큰을 예측할때, 그 토큰 자체의 '사전 확률'을 고려하는 것입니다.
즉, 해당 토큰이 일반적으로 얼마나 자주 등장하는지를 확률로 반영하는 개념이에요.
이를 통해 언어 모델에서 output prior를 사용하면, 어떤 애매모호함을 수학적으로 증명할 수 있습니다.
예를 들어 과일 가게에 가서 ___ 을 샀어요.
__ 에는 사실상 온 갖 종류의 과일, 야채, 심지어 학용품이 들어가도 문법적으로 틀린 말은 아닙니다.
하지만, 🍅가 가장 적절해! 이렇게 얘기하려면 근거가 필요하겠죠?
그런 근거, 즉 확률값, 우리는 output prior를 통해 토마토가 가장 높은 확률값을 가진다고 계산할 수 있습니다.
본 논문에서 output prior 계산식은 총 2가지 항으로 이루어져 있습니다. 첫번째 항은 해당 토큰 자체가 등장할 확률을 의미하고, 두번째 항은 다른 토큰 들과의 관계를 나타냅니다. (다른 토큰들이 등장했을 때, 해당 토큰이 등장할 확률)
한가지 더 궁금한 점이 생깁니다.
어? 주어진 토큰들에 대해 다음 토큰을 예측하는건 자기회귀 모델도 마찬가지 아닌가?
가장 큰 차이점은 확산 모델의 경우, 순차적 예측이 아닌 특정 토큰이 다른 토큰들과 어떤 관계를 가지는지 계산한다는 점입니다. (두번째 항)
3.4 Learned conditional likelihood
손실 함수를 계산하는 과정에서 분산을 최소화하는 방법에 대해 설명하고 있습니다.
손실 함수의 분산을 최소화하기 위해, 두 손실 항목의 분산 비율을 고려하여 학습 데이터를 적절히 할당하는 기법을 사용합니다.
(대충 모델이 안정적으로 학습할 수 있도록 설계했다! 이렇게 이해하고 넘어갔습니다.)
3.5 Self-conditioning
확산 모델의 성능 향상을 위해 self-conditioning 기법을 사용합니다.
self-conditiong 기법은 다음과 같은 특징을 가지고 있습니다.
1. 고정점 반복 구조를 통해 보다 정확한 복원 결과를 얻을 수 있음
2. 학습 시 무작위 전개와 그래디언트 차단을 통해 과도한 계산을 막고 불안정한 학습을 방지함
3. 평가 시 고정된 고정점을 근사하여 모델의 일관성을 확보함
논문에서는 denoiser를 fixed point로 사용하는게 핵심이라고 표현하고 있는데, 이게 또 무슨 의미일까 생각을 해봤습니다.
확산모델은 거듭해서 복원 과정을 거치는데, 복원 과정에서 치팅할 수 있는 무언가가 있구나 이렇게 해석했어요.
예를 들어 시험을 보는데, 매번 처음 부터 다시 다 풀려면 시간도 많이 걸리고, 계산도 많아지고, 또 풀 때 마다 결과가 달라질 수 있겠죠?
근데 만약 내가 확실히 알고 있는 문제는 답안을 지우지 않고, 헷갈리는 문제만 계속 다시 푼다면?
훨씬 빨리 풀 수 있을거예요.
4 Ablation experiments
4.2 Validating algorithmic components
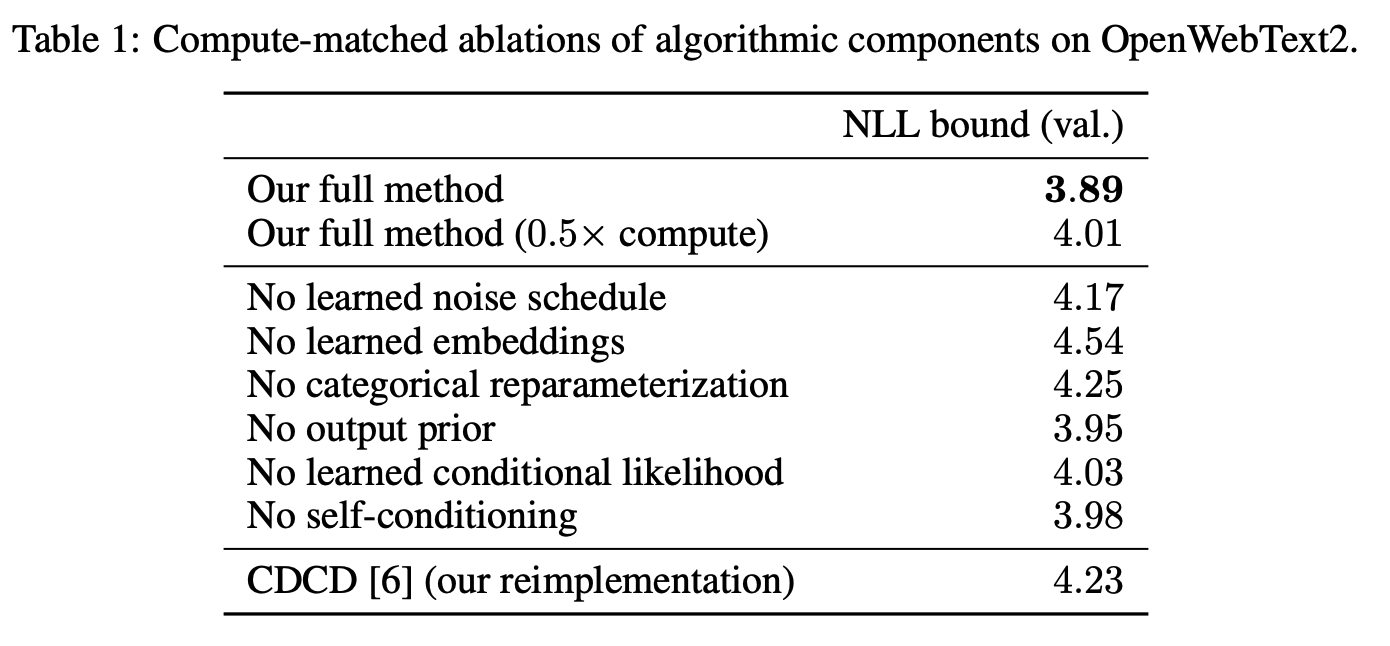
평가지표로 음수로그가능도를 사용하고 있기 때문에 값이 낮을 수록 좋은 모델이라고 평가할 수 있습니다.
모든 요소를 모두 사용했을 때, 가장 성능이 좋을 것으로 보아 각 요소가 유의미하다고 생각할 수 있습니다.
특히, 계산량을 절반으로 줄였을때도 성능이 크게 떨어지지 않는 것으로 보아 연산 효율성도 좋다고 평가할 수 있습니다.
5 Scaling laws for Plaid
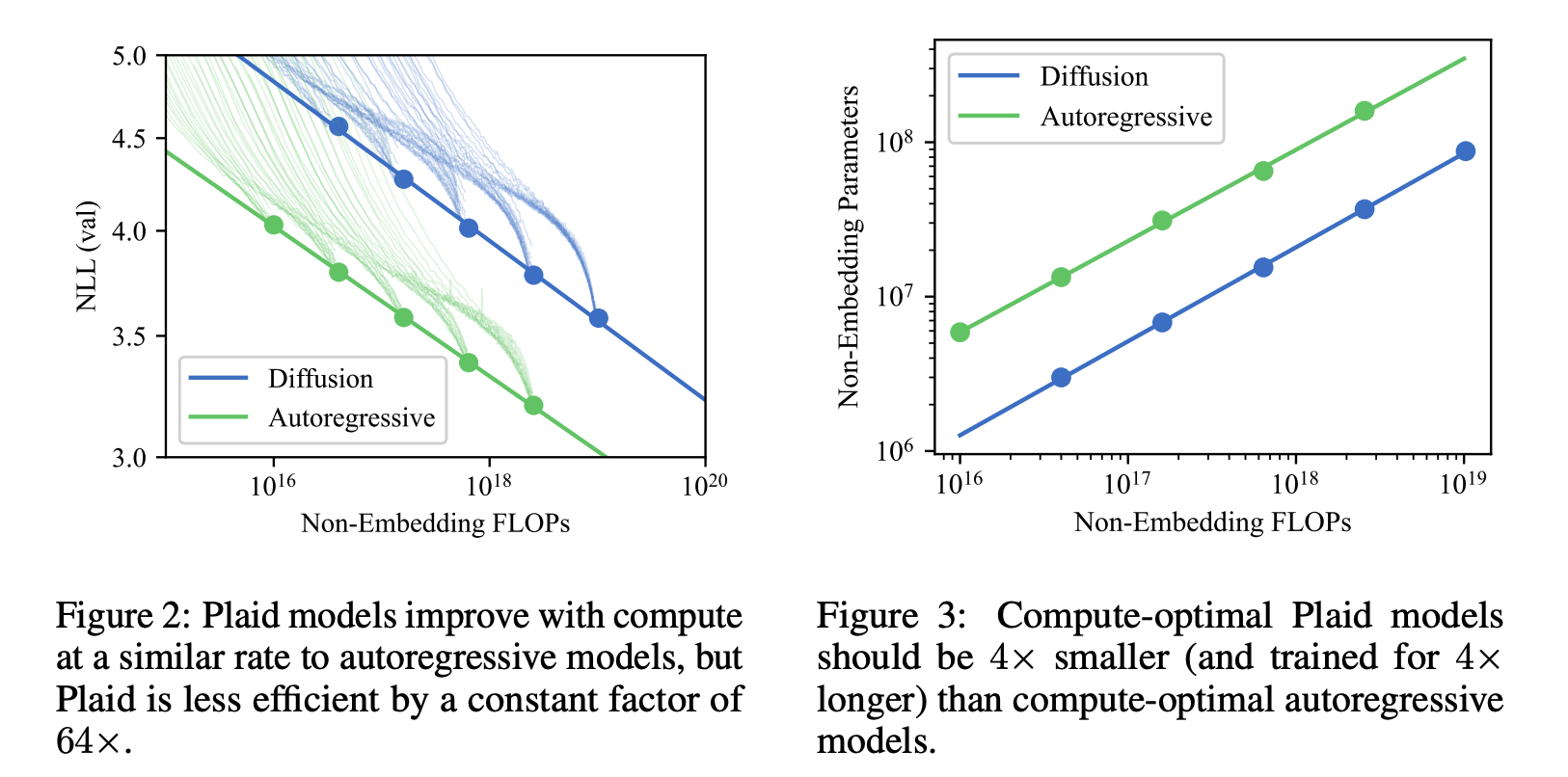
제가 고통받으며 이 논문을 읽은 핵심 부분이 드디어 나옵니다.
과연 확산 모델은 자기회귀 모델과 비교했을 때 어떤 성능을 보일까?
이를 위해 논문에서는 IsoFLOP이라는 분석 기법을 사용하는데, IsoFLOP이란 컴퓨팅 비용 (연산량)을 일정하게 고정한 상태에서 모델 성능을 비교하는 분석 방법입니다. 동일한 FLOP (연산량)을 사용하는 다양한 모델들의 성능을 비교해서 컴퓨팅 효율성을 평가하고 최적의 모델크기 및 학습 전략을 찾을 수 있습니다.
FLOPs를 기반으로 이런 의사 결정이 가능한지 몰랐어요.
Figure2 결과를 보면, Plaid 모델이 기존 자기회귀 모델에 비해 약 64배 더 많은 계산 비용이 필요함을 알 수 있습니다. 즉, 확산 모델이 학습에 더 많은 계산을 필요로 한다는 의미입니다. 그럼에도 불구하고, Plaid 모델이 컴퓨팅 비용이 커질수록 성능이 선형적으로 향상하는 것은 앞으로 성능이 향상할 수 있음을 시사합니다. (논문에서 Scaling law라고 표현하고 있는데 scalability로 이해하면 될 것 같아요. 모델이 커질수록 성능도 향상한다는 바로 그 내용입니다.)
Figure3은 모델의 파라미터 수 대비 FLOPs를 비교하는 그래프입니다. 즉, 모델의 크기와 계산 효율성의 관계를 나타냅니다. 확산 모델은 자기회귀 모델보다 약 4배 작은 크기로 학습해야 효율적이며, 비슷한 성능을 내기 위해선 4배 더 많은 학습 시간을 필요로 합니다. 즉, 확산 모델이 더 작은 파라미터로 더 많은 반복 학습을 해야 성능을 높일 수 있음을 시사합니다. (노이즈 제거 반복 과정이 많으면 많을수록 좋다는 의미일까요??)
6 Plaid 1B
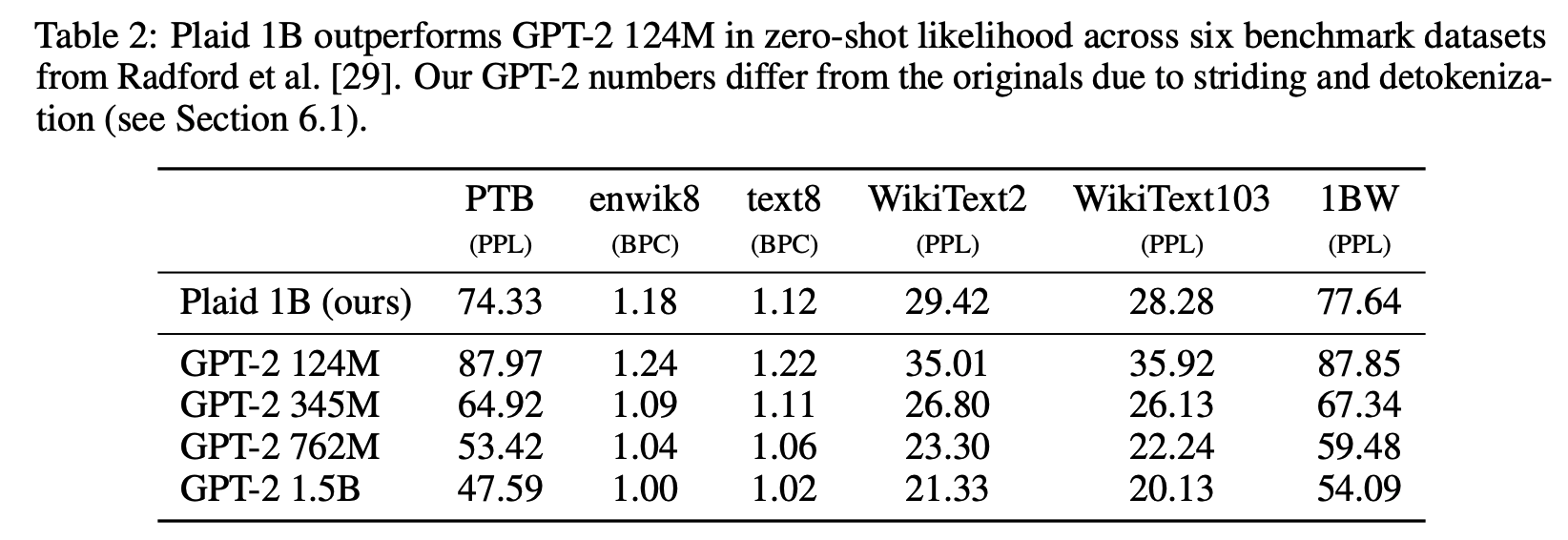
보다 다양한 데이터셋을 기반으로 Plaid 모델을 평가하고 이를 기존 자기회귀 모델과 비교합니다.
평가지표는 Perplexity로 값이 낮을수록 모델의 성능이 우수함을 의미합니다.
비록 비슷한 크기의 자기회귀 모델에 비해서는 성능 차이가 있지만, 작은 크기의 자기회귀 모델 (GPT-2 124M)과는 비슷한 성능을 보입니다.
(제가 생각했을때, 확산 모델의 장점은 학습 이후, inference 시 얼마나 빠른 속도로 답변을 처리할 수 있느냐에 있는 것 같은데, 이런 비교가 따로 이뤄지지 않아 좀 아쉬웠습니다.)
Conclusion에서는 앞선 내용의 반복이라 따로 작성하지 않았습니다.
이미 너무 많이 작성해서 귀찮아서 그런거예요. (솔직)
어찌보면 다양한 결과라고 생각합니다.
본래 LLM을 학습 시킬 때, encoder-decoder 구조에서 encoder를 과감하게 버리고 decoder만을 챙겨갔던건 학습 효율성 때문이었잖아요?
그런 측면을 생각하면, auto-regressiv한 방식은 어쩌다 얻어걸린 방식이라기 보다는 많은 경험과 실험을 기반으로한 결과라고 생각되거든요.
해당 논문의 장점은 auto-regressive 모델과의 (거의) 동등한 비교, 그리고 continous diffusion 모델에 대한 깊은 설명 (너무 고통스러웠어요).
하지만, diffusion 모델의 장점이라고 할 수 있는 다른 성능에 대한 평가 부분이 조금 아쉬웠던 것 같습니다.

논문 마셨어
취했어
'Paper Review > Large Language Model (LLM)' 카테고리의 다른 글
| [논문리뷰] Simple and Effective Masked Diffusion Language Models (1) | 2025.03.21 |
|---|---|
| [논문리뷰] Large Language Diffusion Models (1) | 2025.03.19 |
| [논문리뷰] DeepSeek-V3 Technical Report (4) | 2025.02.04 |
| [논문리뷰] LoRA Learns Less and Forgets Less (1) | 2025.02.03 |
| [논문리뷰] Searching for Best Practices in Retrieval-Augmented Generation (1) | 2025.01.01 |